Area Of A Cylinder By Radius And Height

function Area_Of_A_Cylinder_By_Radius_And_Height(r,h )= 
    2*(PI*r*r)+ 2*PI*r*h;
 

Area Of A Ellipsoid By Radius

Approximation

function Area_Of_A_Ellipsoid_By_Radius(r1,r2,r3 )=  
    4 * PI * pow(((r1*1.6075*r2*1.6075 + r1*1.6075*r3*1.6075
    + r2*1.6075*r3*1.6075)/3),1/1.6075);
 

Area Of A Sphere By Radius

function Area_Of_A_Sphere_By_Radius(r)=  4 *PI* r*r ;

 

Area Of A Cuboid By Sides

function Area_Of_A_Cuboid_By_Sides(A,B,C)=2*(A*B+A*C+C*B);

Area Of A Irregular Polygon By Points

function  Area_Of_A_Irregular_Polygon_By_Points(points, i=1) =
    let(
    area = (points [i-1].x+points[i].x) * (points[i-1].y-points[i].y))
    i<len(points)?
    area/2 +Area_Of_A_Irregular_Polygon_By_Points(points, i+1) 
    :(points [i-1].x+points[0].x) * (points[i-1].y-points[0].y)/2; 


 

Fictional Latin Name Generator

Generate made up latin sounding scientific names.

name = Name_Me();
echo(name);

function Name_Me() = str(
  prefyx1[intrnd(len(prefyx1))],
  suffyx1[ intrnd(len(suffyx1))],
  " ",
  prefyx2[intrnd(len(prefyx2))],
  suffyx2[intrnd(len(suffyx2))]);

function intrnd(a = 0,b = 1) = round((rands(min(a,b),max(a,b),1)[
  0]));
prefyx1 = ["Porodys","Folcam","Cmyd","Prct","Tit","Sog","Prat",
  "Broch","Hidr","Chymch","Spernaph","Lic","Cov","Ol","Ton",
  "Lotr","Psytt","Akop","Nirnec","Gar","Desnad","Gollym",
  "Av","Ephen","Lyss","Pmys","Thil","Helag","Dran","Glyr",
  "Roph","Achat","Phos","Con","Nelaps","Ochot","Struth",
  "Ysapt","Peron","Plotom","Cript","Borb","Vulp","Nesacr",
  "Corch","Log","Sinph","Oepic","Dosip","Banb","Nyr","Pamg",
  "Denasp","Pholomger","Lucom","Ppad","Tryd","Erithr","Pomth",
  "Rhymac","Nomdr","Nocr","Chonoel","Electr","Hypp","Scarp",
  "Coc","Chlar","Squol","Hinem","Phicad","Pov","Caroc",
  "Pstr","Vor","Freg","Cerot","Lep","Tetroad","Onb","Aryal",
  "Meaf","Pigasc","Gerb","Dyan","Holych","Astr","Enid",
  "Lept","Teuth","Om","Gymglin","Dypt","Heleyap","Arict",
  "Munyd","Rom","Ymdr","Chal","Stryg","Negopt","Coyn",
  "Pelec","Phisygm","Crac","Boloem","Vyv","Halath","Syn",
  "Chelam","Rhymad","Syluryf","Bas","Popylyam","Eud","Cyrr",
  "Pr","Tragl","Goleac","Demdrabr","Pryst","Nuroem","Serp",
  "Pratar","Cost","Lusc","Lon","Oylur","Tochig","Sorcaph",
  "Buf","Chlon","Sphem","Hil","Phac","Porol","Caleapt","Prd",
  "Urapl","Farnyc","Cephol","Leamtap","Olcel","Tors","Pteran",
  "Aphys","Mos","Gul","Gekkam","Dycer","Recurv","Limx",
  "Adab","Heter","Cett","Dim","Laphal","Tren","Pp","Pogur",
  "Ereth","Ner","Copr","Loc","Oct","Suryc","Cigm","Net",
  "Bys","Pag","Phoeth","Doubemt","Pelaph","Pyc","Cracad",
  "Vanb","Bolsem","Och","Stryx","Yms","Neleogr","Coll",
  "Romg","Asteal","Micter","Helad","Gyr","Droc","Ator","Emh",
  "Lynul","Threskyarm","Omg","Pseud","Set","Nust","Prac",
  "Goll","Dern","Coud","Lutr","Lorv","Oj","Tolp","Cyvett",
  "Prochm","Turs","Poroch","Eupt","Han","Chyl","Snyl",
  "Rupyc","Cet","Br","Poss","Phaemyc","Prv","Urs","Canmach",
  "Scyur","But","Hilab","Chlonid","Sphir","Frot","Cer",
  "Leap","Oll","Tox","Arc","Mectaphr","Pigac","Ginmyd",
  "Geach","Dyd","Rhymc","Adac","Noc","Hyer","Choetad",
  "Echym","Pom","Eryth","Laxad","Ppot","Trych","Nesabotr",
  "Cor","Locert","Oeg","Sus","Dos","Blott","Nycrac","Phol",
  "Delph","Panoc","Cat","Ptel","Vesp","Pec","Phis","Negod",
  "Coel","Yguom","Stegast","Chaer","Fum","Eleuther","Lepys",
  "Tetroam","Onphypr","Mephr","Armytharh","Ronph","Hel",
  "Gerr","Dypl","Pop","Es","Cychl","Pptem","Trach",
  "Rhymacer","Nomnuth","Nomt","Hyppap","Chel","Eleph",
  "Ocomth","Cos","Logemarh","Oyl","Simc","Sep","Nal","Lemn",
  "Pryam","Demdrab","Phoran","Pog","Eq","Lyt","Trogel",
  "Pmth","Rott","Phoscal","Actap","Henyg","Gaph","Dug",
  "Lobr","Ocym","Sul","Neph","Com","Paec","Iso","Phocach",
  "Cuam","Bett","Xemap","Groid","Gov","Dyc","Amysc","Momd",
  "Pter","Top","Olc","Len","Ceb","Fel","Caccym","Prctac",
  "Urach","Porodax","Phosnot","Soyn","Bub","Hidrad","Chyrapt",
  "Sph"];
prefyx2 = ["Vulp","Bym","Phis","Nol","Escul","Yguom","Splemd",
  "Delyc","Corch","Grouer","Nuscul","Rydyb","Mad","Lotr",
  "Tybet","Onphyb","Umyc","Otr","Arm","Lup","Scomd","Cat",
  "Danest","Herc","Pumct","Nelom","But","Oeg","Fusc","Olb",
  "Silv","Jub","Farst","Ogoss","Sun","Fonyl","Ymdr","Ocomth",
  "Barm","Papul","Nor","Goiom","Chris","Rubec","Cyv","Leuc",
  "Aedyp","Tragl","Or","Cumyc","Syn","Electr","Harr","Vytul",
  "Borb","Nocrac","Pord","Quogg","Nym","Conelap","Gyg","Olp",
  "Tour","Mott","Log","Cicl","Sph","Hidrach","Eq","Valyt",
  "Ber","Pot","Nogorh","Tenpar","Onblirh","Mghetymh","Lomyg",
  "Rott","Nul","Copuc","Glon","Ar","Lat","Tip","Org","Camc",
  "Rupyc","Dymg","Hobrapt","Bub","Ocutar","Fulg","Pryn",
  "Noxyn","Jocks","Foscyc","Suryc","Oj","Pyct","Nomd","Zerd",
  "Byr","Streps","Den","Euric","Ynper","Omg","Tac","Lept",
  "Abscur","Ras","Cym","Grunm","Cott","Piger","Neph","Coff",
  "Gomget","Olc","Tomg","Fromc","Kanad","Pom","Limx","Vym",
  "Oxelr","Draned","Hyrc","Sciph","Crac","Spylag","Dorw",
  "Yb","Ern","Vulg","Byc","Potog","Nogell","Myv","Lorv",
  "Tetr","Onaiems","Retyc","Nur","Cor","Gar","Lun","Arc",
  "Umdul","Os","Sop","Carb","Dyph","Horr","Fer","Jahmst",
  "Ol","Susp","Nel","Praciam","Buf","Odel","Fur","Plotirh",
  "Nomdt","Obel","Bysam","Sulfur","Derb","Folcam","Ymd",
  "Tryd","Omtyp","Accyd","Less","Rasn","Cyrr","Grip","Cemtr",
  "Vytt","Boctr","Pop","No","Dug","Haffn","Cucull","Serv",
  "Tor","Olysn","Zig","Loev","Pign","Nyd","Conel","Geaffr",
  "Bymt","Zebr","Nom","Pyc","Delph","Str","Eurap","Ymn",
  "Lemn","Mavoeomgl","Tygr","Omot","Rabust","Mos","Cotesb",
  "Grev","Poln","Lutr","Ursym","Our","Hern","Dars","Scr",
  "Cryst","Put","Nemd","Cob","Ofr","Goll","Toj","Olbyv",
  "Frog","Kymg","Meb","Logatr","Tox","Olt","Rodyot","Namoch",
  "Gygomt","Cop","Vyverr","Bemgol","Porv","Nocul","Eleg",
  "Hunb","Samd","Cuv","Sunotr","Ogyl","Fosc","Yr","Broch",
  "Ocul","Ful","Noxyll","Parc","Trumc","Orct","Amc","Lyber",
  "Dyehl","Gul","Ruf","Calch"];
suffyx1 = ["ebus","echus","ecto","edeydoe","eydoe","eyradam",
  "elo","eles","elys","ello","ellydoe","elame","elphys",
  "elus","enus","emtes","emtrus","emus","ea","eamydoe",
  "epholymoe","ero","erculo","erda","erydoe","eryx","erno",
  "eraptero","eras","erro","erto","erus","es","eter","eus",
  "eutes","yo","yolys","yomus","yos","ycetus","ychthis",
  "ycalo","yctys","ydo","ydoe","ydeo","yfer","yfero",
  "yfarne","ygotar","yido","yidoe","yifarnes","ylyo","ylydoe",
  "yllo","yllymoe","yllus","ylatys","ylus","amtymoe","amix",
  "apex","aphogo","apharus","aphris","apydoe","apado",
  "apracto","aps","ojoa","ole","olys","olus","onolys",
  "onbulus","omchyoto","omger","omymoe","omto","omthydoe",
  "omtulus","omus","oam","ophymoe","ophus","opro","optero",
  "orctas","ordus","orhymus","ory","oryo","oradam","os",
  "ostes","ostas","oto","othus","otydoe","otymo","otus",
  "ourus","ovyo","eoster","aotus","athryx","atydoe","atrytam",
  "auotto","aumgo","ax","azao","uo","uoryus","oimus","ois",
  "ulo","uno","ur","uro","urgo","urydoe","apsys","aptero",
  "apterus","apus","ar","ardoto","arhymus","aryo","arnes",
  "arus","arix","asourus","asteydoe","astano","atonus",
  "atheryun","oco","ocol","ochyo","ochrus","ocyme","ocmo",
  "ocus","oe","oeydoe","oenus","oemo","oemydoe","oetes",
  "offo","oylurus","oyus","ojo","urmyx","uraydeo","urus",
  "us","uto","uus","iotys","idro","idrydoe","yimy","ilox",
  "ilus","imchus","ime","inmys","iam","ipelno","ipharus",
  "ipyus","iptes","iptulo","irmo","isadam","istano","iuro",
  "iurus","ymo","ymoe","ymy","ymyo","ymydyo","ymaydeo",
  "ymus","ya","yaydeo","yames","yamymoe","yaps","ypedyo",
  "yry","yrastro","yrus","ys","yscus","ystaydeo","ythecus",
  "ythydoe","ythades","ythryx","ytys","yttocus","yus","yzam",
  "lassus","a","abyus","aconpo","aconpus","acebus","ach",
  "achelis","achaerus","adoctilus","adeo","adectus","adydoe",
  "adam","adamtus","adites","aepus","aerus","agole","aydeo",
  "ayleus","ays","alogus","ano","anarpho","am","amo","amg",
  "amgyoe","amyo","amyx","amto","amtydoe"];
suffyx2 = ["amix","apus","ar","aryus","armys","as","astroto",
  "astrys","asus","atoto","atys","auro","auxyi","ax","ayi",
  "azao","uo","uca","ues","oimus","otycus","otar","yomus",
  "yorys","yos","yotun","yotus","yblys","yco","yceps",
  "yceras","ycho","yculus","ycus","ydus","yems","yemsys",
  "yer","yes","ygemyus","yi","ylys","yllo","ylus","ymo",
  "ymeo","ymyi","ymaso","ymun","ymus","ymx","yal","yaso",
  "ys","yscy","yscus","ysyi","ytynus","ytys","yus","yzyi",
  "a","acane","ades","ady","adytus","adites","aemsys","afo",
  "aydes","aldty","aleuco","alaphus","alar","am","amoe",
  "ame","amy","amycus","amyi","otroe","otto","otu","otun",
  "otus","oun","oiomus","eo","eotus","ol","olyo","olys",
  "ollus","olumgo","olus","onpus","om","omdus","omy",
  "omycus","oms","omus","opro","ordolys","oryo","oryos",
  "orymyo","orys","oryus","orun","orus","os","ospys","oster",
  "otolo","iurus","ectun","eemsys","eyomo","elyo","ellus",
  "emgey","ems","emsys","emtolys","emteus","emtrys","emtus",
  "ea","epholus","er","ero","erery","ereus","ery","eryo",
  "ersus","erus","es","etto","etty","eus","yocus","yoe",
  "ulo","ulorys","uloto","ules","ulaso","ulus","un","umdus",
  "urmyx","uramg","us","uto","uus","iomus","yi","imchas",
  "ithrus","ocol","octilo","ocu","oeo","oemo","oerys","oeus",
  "ogrus","oyco","oycus","ojo"];


 



 

Area Of A Regular Polygon By Radius And N

function Area_Of_A_Regular_Polygon_By_Radius_And_N(r,N)=
    (r*r*N*sin(360/N))/2;


 

Named Colors Indexable List

Generate a list of OpenScad named colors.

function colors()= [
"Lavender", 
"Thistle", 
"Plum", 
"Violet", 
"Orchid", 
"Fuchsia", 
"Magenta", 
"MediumOrchid", 
"MediumPurple", 
"BlueViolet", 
"DarkViolet", 
"DarkOrchid", 
"DarkMagenta", 
"Purple", 
"Indigo", 
"DarkSlateBlue", 
"SlateBlue", 
"MediumSlateBlue", 
"Pink", 
"LightPink", 
"HotPink", 
"DeepPink", 
"MediumVioletRed", 
"PaleVioletRed", 
"Aqua", 
"Cyan", 
"LightCyan", 
"PaleTurquoise", 
"Aquamarine", 
"Turquoise", 
"MediumTurquoise", 
"DarkTurquoise", 
"CadetBlue", 
"SteelBlue", 
"LightSteelBlue", 
"PowderBlue", 
"LightBlue", 
"SkyBlue", 
"LightSkyBlue", 
"DeepSkyBlue", 
"DodgerBlue", 
"CornflowerBlue", 
"RoyalBlue", 
"Blue", 
"MediumBlue", 
"DarkBlue", 
"Navy", 
"MidnightBlue", 
"IndianRed", 
"LightCoral", 
"Salmon", 
"DarkSalmon", 
"LightSalmon", 
"Red", 
"Crimson", 
"FireBrick", 
"DarkRed", 
"GreenYellow", 
"Chartreuse", 
"LawnGreen", 
"Lime", 
"LimeGreen", 
"PaleGreen", 
"LightGreen", 
"MediumSpringGreen", 
"SpringGreen", 
"MediumSeaGreen", 
"SeaGreen", 
"ForestGreen", 
"Green", 
"DarkGreen", 
"YellowGreen", 
"OliveDrab", 
"Olive", 
"DarkOliveGreen", 
"MediumAquamarine", 
"DarkSeaGreen", 
"LightSeaGreen", 
"DarkCyan", 
"Teal", 
"LightSalmon", 
"Coral", 
"Tomato", 
"OrangeRed", 
"DarkOrange", 
"Orange", 
"Gold", 
"Yellow", 
"LightYellow", 
"LemonChiffon", 
"LightGoldenrodYellow", 
"PapayaWhip", 
"Moccasin", 
"PeachPuff", 
"PaleGoldenrod", 
"Khaki", 
"DarkKhaki", 
"Cornsilk", 
"BlanchedAlmond", 
"Bisque", 
"NavajoWhite", 
"Wheat", 
"BurlyWood", 
"Tan", 
"RosyBrown", 
"SandyBrown", 
"Goldenrod", 
"DarkGoldenrod", 
"Peru", 
"Chocolate", 
"SaddleBrown", 
"Sienna", 
"Brown", 
"Maroon", 
"White", 
"Snow", 
"Honeydew", 
"MintCream", 
"Azure", 
"AliceBlue", 
"GhostWhite", 
"WhiteSmoke", 
"Seashell", 
"Beige", 
"OldLace", 
"FloralWhite", 
"Ivory", 
"AntiqueWhite", 
"Linen", 
"LavenderBlush", 
"MistyRose", 
"Gainsboro", 
"LightGrey", 
"Silver", 
"DarkGray", 
"Gray", 
"DimGray", 
"LightSlateGray", 
"SlateGray", 
"DarkSlateGray", 
"Black"
];
 

Area Of A Regular Polygon By Side And N

function Area_Of_A_Regular_Polygon_By_Side_And_N(A,N)=
     A*A*N/(4*tan(180/N));
 

Great Circle / Concentric Small Circle By Two Lat Long Points

A great circle is any circle drawn on a  sphere with a center at the center of the sphere and thus the same radius.

function face_normal(point_a,point_b,point_c)=
let(u=point_a-point_b,v=point_a-point_c)
un([u[1]*v[2]-u[2]*v[1],u[2]*v[0]-
u[0]*v[2],u[0]*v[1]-u[1]*v[0]]);

function un(v)=v/max(norm(v),1e-64);

function look_at(p,o=[0,0,0],up=[0,0,1])=
let(
a=up,
b=p-o,
c=cross(a,b) ,
d=angle(a,b))
[d,c];

function angle (a,b)=
atan2(
sqrt((cross(a, b)*cross(a, b))), 
(a* b)  );

function rnd(a = 1, b = 0, s = []) =
s == [] ?
(rands(min(a, b), max(
a, b), 1)[0]) :
(rands(min(a, b), max(a, b), 1, s)[0]);

function Great_circle_axis(p1,p2,r)=
let(v1=face_normal([0,0,0],p1,p2))
v1;

module Great_circle(p1,p2,r){
v1=face_normal([0,0,0],p1,p2);
look_at(v1)torus(r,0.05);
}
module Concentric_small_circle(p1,p2,r,r2){
v1=face_normal([0,0,0],p1,p2);
look_at(v1)translate([0,0,sign(r2)*r*cos(90*(r2/r))])
torus(r*sin(90*(r2/r)),0.05);
}

module torus(r1,r2)
{rotate_extrude($fn=40)translate([r1,0,0])circle(r2,$fn=12);
}
module look_at(lookpoint,origin=[0,0,0],rotatefrom=[0,0,1]){
rotations=look_at(lookpoint,origin ,rotatefrom);
rotate(rotations[0],rotations[1]) children();
}
radius=5;
small_radius=radius*rnd();
#sphere(5,$fn=40);
lat1=rnd(-90,90);
long1=rnd(0,360);
lat2=rnd(-90,90);
long2=rnd(0,360);

p1= ([sin(long1),cos(long1)*sin(lat1),cos(lat1)])*radius;
p2= ([sin(long2),cos(long2)*sin(lat2),cos(lat2)])*radius;
echo(p1,p2);
translate(p1) sphere(0.3,$fn=40);
translate(p2) sphere(0.3,$fn=40);

Great_circle(p1,p2,radius);
Concentric_small_circle(p1,p2,radius,-small_radius);
Concentric_small_circle(p1,p2,radius,small_radius);

Compounded Interest On Principal

Final_Amount: The future amount including compounded interest
Principal: The starting amount
rate: interest rate in decimal  
n:the number of times that interest is compounded per year
time: the number of years the amount is compounded
https://goo.gl/sXRkHQ
Usage:

function Compounded_Interest(Principal,rate,n,time)=let(
Final_Amount =Principal *pow( (1 + rate/n) , n*time) )
Final_Amount;

echo(100,Compounded_Interest(100,0.05,1,10));

Challenge 1: Can you make a diagram displaying the growth month by  month?
 
Challenge 2: What if you add in a monthly saving?

Area Of A Ellipse By Radius

function Area_Of_A_Ellipse_By_Radius(r1,r2)=r1*r2*PI;


 

Great-Circle Distance between two lat long positions

This formula doesn't count the flattening of the earth at the poles. 
The earth has been approximated to a sphere with a radius of 6378 km.
 

function Great_circle_distance(latA,longA,latB,longB) =   
acos ( 
sin (latA) * sin (latB) +
cos (latA) * cos (latB) * cos (longB - longA) 
)*111.195  ;//(6371/57.295779513)

echo (Great_circle_distance(48.8566, -2.3522,52.5200 , -13.4050) );

//INFERNAL ;)
echo (Great_circle_distance(0, 90, 0, 0) );
 
 

Area Of A Circle By Radius

function Area_Of_A_Circle_By_Radius(r)=r*r*PI;


 

Points inside a cube

Generates a list of random points that lie inside a cuboid.

function random_points_inside_cuboid(p1,p2,n)=

    [for(i=[1:n])cuboid_point(p1,p2)];

function cuboid_point(p1,p2)= 

  [rands(-p1.x,p2.x,1)[0],

   rands(-p1.y,p2.y,1)[0],

   rands(-p1.z,p2.z,1)[0]] ;

p1=[0,0,0];
p2=[100,100,100];
p=random_points_inside_cuboid(p1,p2,1000);
for(t=p)translate(t)sphere(4);
echo(p);
 

Area Of A Rectangle By Sides

function Area_Of_A_Rectangle_By_Sides(A,B)=A*B;


 

Stone wall brick offset calculations

(Layers mod 2) equals zero at even layers 
and one for uneven layers.
wikipedia.org/wiki/Modulo_operation
Challenge: What other brick patterns can you make?

brick_length=5;
half_brick_length=brick_length/2;
brick_width=3;
brick_height=2;

for(layer=[0:1:5])
for(run=[0:1:5]){
shift= layer % 2; // <-- this is the sauce
translate(

[run*brick_length+shift*half_brick_length,

0,

layer*brick_height])

brick();
}

module brick(){color(rands(0,1,3)) 
cube([brick_length,brick_width,brick_height]);}
 

Area Of A Equilateral Triangle By Side

function Area_Of_A_Equilateral_Triangle_By_Side(A)= sqrt(3)/4 *(A*A);

Check out the openscad links and resources page

Find out more about openscad 

 

https://openscadsnippetpad.blogspot.se/p/openscad-links.html

Area Of A Triangle By Base And Height

function Area_Of_A_Triangle_By_Base_And_Height(A,h)=(1/2)*A*h;

Area Of A Triangle By Sides

Description here Usage:

function Area_Of_A_Triangle_By_Sides(a,b,c)=
    let(s=(a+b+c)/2) sqrt(abs(s*(s-a)*(s-b)*(s-c)));

Points inside a sphere

Generates a list of random points that lie inside a sphere

function random_points_inside_sphere(r,n)=

[for(i=[1:n])sphere_point(r)];

function sphere_point(r)=

let (p=rands(-r,r,3)) 

(pow(p.x,2) + pow(p.y,2) + pow(p.z,2) > pow(r,2))?sphere_point(r):p;


p=random_points_inside_sphere(50,1000);
for(t=p)translate(t)sphere(4);
echo(p);

Perimeter Of A Irregular Polygon By Points

function Perimeter_Of_A_Irregular_Polygon_By_Points(points, i=1) =

let(   
     Side = (norm(points[i]-points[i-1])))
    i<len(points)?Side 

+Perimeter_Of_A_Irregular_Polygon_By_Points(points, i+1) 

:(norm(points[0]-points[i-1])); 

Perimeter Of A Regular Polygon By Inradius And N

function Perimeter_Of_A_Regular_Polygon_By_Inradius_And_N(r,N)= 
  2*N*r*tan(180/N);

Perimeter Of A Regular Polygon By Radius And N

function Perimeter_Of_A_Regular_Polygon_By_Radius_And_N(r,N)= 
     2*N*r*sin(180/N);
 

Perimeter Of A Regular Polygon By Side And N

function Perimeter_Of_A_Regular_Polygon_By_Side_And_N(A,N)= A*N;

Perimeter Of A Ellipse By Radius

function Perimeter_Of_A_Ellipse_By_Radius(r1,r2)=
    PI*(3*(r1+r2)-sqrt((3*r1+r2)*(r1+3*r2)));
 

Perimeter Of A Circle By Radius

function Perimeter_Of_A_Circle_By_Radius(r)=2*PI*r;

Perimeter Of A Rectangle By Sides

function Perimeter_Of_A_Rectangle_By_Sides(A,B)=A+A+B+B;

 

Perimeter Of A Isosceles Triangle By Base And Height

function Perimeter_Of_A_Isosceles_Triangle_By_Base_And_Height
    (A,h)= A*sqrt((a/2)*(a/2)+h*h);
 

Square / Rectangle Path

Generates a path in the shape of a rectangle .
Steps are rounded to evens for obvious reasons
Usage:

function figureL7(x=40,y=20,step=52)=
let(total=(x+x+y+y),steps_x=round(step/total*x),steps_y=round(step/total*y))
concat(
[for(t=[0:steps_x-1])[(-x/2+(x/steps_x)*t),y/2]],
[for(t=[0:steps_y-1])[x/2,y/2-((y/steps_y)*t)]],
[for(t=[0:steps_x-1])[x/2-((x/steps_x)*t),-y/2]],
[for(t=[0:steps_y-1])[-x/2,-y/2+(y/steps_y)*t]]);

function close(p)=concat(p,[p[0]]);
module polyline(p){for(i=[0:max(0,len(p)-2)])color([i%2])line(p[i],p[i+1]);}
module line(p1,p2,width=0.5){hull(){
    translate(p1)sphere(width);
    translate(p2)sphere(width);}}


polyline(close(figureL7()));
 
 

Circle Path

Generates a path in the shape of a circle

 
function circle(r=100,steps=100)=
[ for(t=[0:1/steps:1])
let(  x =r* sin(t*360),   y =r*cos(t*360)  )
[x,y] ];

// function close adds a last point equal yo the first


function close(p)= concat(p,[p[0]]);


module polyline(p) {for(i=[0:max(0,len(p)-2)])line(p[i],p[i+1]);}
module line(p1, p2 ,width=0.5) 
{
    hull() {
        translate(p1) sphere(width);
        translate(p2) sphere(width);
    }
}


polyline(close(circle())); 
 

Figure Eight Path

Generates a path in the shape of figure eight

function figure8(m=100)=[for(t=[0:1:360])
let(scale = 2 / (3 - cos(2*t)),x =m* scale * cos(t),y =m* scale * sin(2*t) / 2)
[x,y]];

function close(p)= concat(p,[p[0]]);

module polyline(p) {for(i=[0:max(0,len(p)-2)])line(p[i],p[i+1]);}
module line(p1, p2 ,width=0.5) 
{
    hull() {
        translate(p1) sphere(width);
        translate(p2) sphere(width);
    }
}


polyline(close(figure8(50))); 


 

Perimeter Of A Equilateral Triangle By Side

function Perimeter_Of_A_Equilateral_Triangle_By_Side(A )=A+A+A ;


 

Pascal Triangle

Find the number on row a and position b of Pascals Triangle.
 Row and  position numbers begin from 0 

function pascalTriangle(a, b,result=1,i=0)=
 
    i<b?  pascalTriangle(a, b,(result * (a-i)/(i+1)),i+1 ) : result;
 
for(a=[0:10])
echo( [for(b=[0:a])pascalTriangle(a,b)] );
 

ECHO: [1]
ECHO: [1, 1]
ECHO: [1, 2, 1]
ECHO: [1, 3, 3, 1]
ECHO: [1, 4, 6, 4, 1]
ECHO: [1, 5, 10, 10, 5, 1]
ECHO: [1, 6, 15, 20, 15, 6, 1]
ECHO: [1, 7, 21, 35, 35, 21, 7, 1]
ECHO: [1, 8, 28, 56, 70, 56, 28, 8, 1]
ECHO: [1, 9, 36, 84, 126, 126, 84, 36, 9, 1]
ECHO: [1, 10, 45, 120, 210, 252, 210, 120, 45, 10, 1]

Perimeter Of A Triangle By Sides

function Perimeter_Of_A_Triangle_By_Sides(A,B,C)=A+B+C;

 

Recursive Tangential Circle Approximation To Any Mix Of 3 Points, Lines, Circles Or Rectangles

Recursively try to find circles that touch outside three random features
of either point, line, circle or rectangle. 

Approximation start at a seed point and steps towards the smaller error 
until the summed error is smaller than a threshold.
First attempt starts at features common average  midpoint. 
If approximation error is smaller than threshold  the search is halted. 

Next starting points from around perimeter are tried and then a bunch of random starting  points.

Solution inside circles and squares hare not handled.
Results are not scientific exact, enough for construction of drawing.
Some unsolved edge cases fail, reducing overall usefulness.


Demo choose random features
Usage:

threshold = 1e-5;
workarea = 100;


function  AcmeSolver(f0, f1, f2, ifind = undef, maxi = 6000) =
let (
find = ifind == undef ? 
    (featurecenter(f0)   + featurecenter(f1)  
    + featurecenter(f2)  ) /3: ifind, 
d0 =distancetofeature(f0, find), 
nf0 = normaltofeature(f0, find),
d1 = distancetofeature(f1, find), 
nf1 = normaltofeature(f1, find),
d2 = distancetofeature(f2, find), 
nf2 = normaltofeature(f2, find),
sum = abs(d0 - d1) + abs(d1 - d2) + abs(d2 - d0), 
avrg = (d0 + d2 +    d1) / 3,  
cf0 = (find + nf0 * (max(0, d0) - avrg) * 0.999),  
cf1 = (    find + nf1 * (max(0, d1) - avrg) * 0.999),  
cf2 = (find + nf2 * (    max(0, d2) - avrg) * 0.999),  
newfind = (cf0 + cf1 + cf2) / 3 )
sum < threshold || maxi < 0 ? 
[find, avrg,   sum]
:  AcmeSolver(f0,
f1, f2, newfind, maxi - 1);

function featurecenter(feat) = 
len(feat) == 2 && len(feat[0]) ==  undef ? feat :
len(feat) == 3 && len(feat[0]) == undef ? [feat.x,feat.y] : 
len(feat) == 2 && len(feat[0]) == 2 ? (feat[0] + feat[1]) /2 :
len(feat) == 2 && len(feat[0]) == 2 ? 
(feat[0] + feat[1]+feat[2] + feat[3]) /  4 : [0, 0];

function distancetofeature(feat, find) = 
len(feat) == 2 && len(feat[0]) ==  undef ? norm(feat - find) : 
len(feat) == 3 && len(feat[0]) == undef ?  
distancetocircle(feat, find) : 
len(feat) == 2 && len(feat[0]) == 2 ?  distancetoline(feat, find) : 
len(feat) == 4 && len(feat[0]) == 2 ?  distancetosquare(feat, find) :
0;

function normaltofeature(feat, find) = 
len(feat) == 2 && len(feat[0]) ==  undef ? normaltopoint(feat, find) :
 len(feat) == 3 && len(feat[0]) ==  undef ? 
normaltocircle(feat, find) : 
len(feat) == 2 && len(feat[0]) ==  2 ? normaltoline(feat, find) :
len(feat) == 4 && len(feat[0]) ==  2 ? normaltosquare(feat, find) :
 0;

function distancetopoint(point, find) = norm(point - find);

function distancetocircle(circle, find) = 
norm([circle.x, circle.y] -  find) - circle[2];

function distancetoline(line, p) =
let (a = line[0], b = line[1], 
pa = p - a, ba = b - a, h =  ((pa * ba) /
  (ba * ba)))norm(pa - ba * h);

function distancetosquare(square, p) =min (
distancetosegment([square[0],square[1]],p),
distancetosegment([square[1],square[2]],p),
distancetosegment([square[2],square[3]],p),
distancetosegment([square[3],square[0]],p)

);

function distancetosegment(line, p) =
let (a = line[0], b = line[1], pa = p - a, ba = b - a,
 h =  clamp((pa * ba) /  (ba * ba)))
norm(pa - ba * h);
function clamp(a, b = 0, c = 1) = min(max(a, b), c); 

function normaltopoint(point, find) = 
(point - find) / norm(point -  find);

function normaltocircle(circle, find) = 
([circle.x, circle.y] - find) /norm([circle.x, circle.y] - find);

function normaltoline(line, find) =
let (a = line[0], b = line[1], dtl2 = distancetoline(line, find))
un([distancetoline(line, find + [-1, 0]) -

 dtl2, distancetoline(line,  find + [0, -1]) - dtl2]);

function normaltosegment(line, find) =
let (a = line[0], b = line[1],c=un(a-b))[-c.y,c.x];
 

function normaltosquare(square, find) =
let (  base = distancetosquare(square, find))
un([distancetosquare(square, find + [-1, 0]) - 

base, distancetosquare(square, find+ [0, -1]) - base]);

function un(v) = v / max(1e-15, norm(v));

// demo code

function allines(f0,f1,f2)=isline(feature0)

&&isline(feature1)&&isline(feature2);

function isline(feat)=len(feat) == 2 

&& len(feat[0]) == 2 ?true:false;
function randomfeature() =
let (s0 = round( rnd(3)
))
(s0 == 0) ? [rnd(workarea), rnd(workarea), rnd(1, workarea * 0.5)] :
(s0 == 1) ? [rnd(workarea), rnd(workarea)] : 
(s0 == 2) ? [[rnd(  workarea), rnd(workarea)],

 [rnd(workarea), rnd(workarea)]] :
(s0 == 3) ? let(

p1=[rnd(workarea), rnd(workarea)],

p2=p1+[rnd(workarea)/2, rnd(workarea)/2],

r=rnd(360),p3=(p1+p2)/2)
[rotp(r,p1,p3),rotp(r,[p2.x,p1.y],p3),

rotp(r,p2,p3),rotp(r,[p1.x,p2.y],p3) ] :
 ["err"];

function rotp(r,ip,p3)=
let( p=ip-p3, s = sin(r),
  c = cos(r),
    xnew = p.x * c - p.y * s,
    ynew = p.x * s + p.y * c)
[xnew,ynew]+p3
;
module showfeature(feat) {
  color("black") {
    if (len(feat) == 2 && len(feat[0]) == undef) {
      echo(" point ", feat);
      translate(feat) sphere(2);
    }
    if (len(feat) == 3 && len(feat[0]) == undef) {
      echo(" circle ", feat);
      linear_extrude(1)translate([feat.x, feat.y]) difference() {
        circle(feat[2]);
        circle(feat[2] - 1);
      }
    }
    if (len(feat) == 2 && len(feat[0]) == 2) {
      echo(" line ", feat);
      linear_extrude(1)hull() {
        translate(feat[0]) circle(1);
        translate(feat[1]) circle(1);
      }
      n1 = un(feat[0] - feat[1]);
      linear_extrude(0.2)hull() {
        translate(feat[0] + n1 * workarea) circle(0.2);
        translate(feat[1] - n1 * workarea) circle(0.2);
      }
    }
if (len(feat) == 4 && len(feat[0]) == 2) {
      echo(" square ", feat);
      linear_extrude(1)hull() {
        translate(feat[0]) circle(0.5);
        translate(feat[1]) circle(0.5);
      }
 linear_extrude(1)hull() {
        translate(feat[1]) circle(0.5);
        translate(feat[2]) circle(0.5);
      }
      linear_extrude(1)hull() {
        translate(feat[2]) circle(0.5);
        translate(feat[3]) circle(0.5);
      }
      linear_extrude(1)hull() {
        translate(feat[3]) circle(0.5);
        translate(feat[0]) circle(0.5);
      }
     
    }
  }
}
module ring(d, i = 1) {
  linear_extrude(i)
  {
    translate(d[0]) difference() {
      circle(d[1], $fn = 60);
      circle(max(0,d[1] - 1), $fn = 60);
    }
  }
}

function rnd(a = 1, b = 0, s = []) = s == [] ? 

(rands(min(a, b), max(
  a, b), 1)[0]) : (rands(min(a, b), max(a, b), 1, s)[0]);



feature0 = randomfeature();
feature1 = randomfeature();
feature2 = randomfeature();
showfeature(feature0);
showfeature(feature1);
showfeature(feature2);
// try fo fit from midpoint
d =  AcmeSolver(feature0, feature1, feature2);
//[center,radius, fit]

if (d[2] < threshold &&!allines(feature0, feature1, feature2)){
echo(" Found Internal ", d);
  color("red") ring(d, 1.5);
}
else {
  color("yellow") ring(d);
  if (d[2] < workarea*0.1) {
    echo(" Found no internal solution in time. Best fit : ", d[2]);
    echo(d);    
  }
  else {
    echo(" Found no internal solution in time. Best approximation : ");
    echo(d);   
  }

// try to fit from ouside
for (i = [45: 90: 360]) {
  cme = [sin(i) * workarea * 10, cos(i) * workarea * 10];
  de =  AcmeSolver(feature0, feature1, feature2, cme,1500);
  if (norm(d[0] - de[0]) > threshold) {
    if (de[2] < threshold) {
      color([1, rnd(), rnd()]) ring(de,0.9);
      echo(" Found External ",de);
    }
    else {
      echo(" Found no external solution in time ");
    }
  }
}
// try to fit from Random State
for (i = [0:  10]) {
  cme = [rnd(-workarea,workarea*2),rnd(-workarea,workarea*2)];
  de =  AcmeSolver(feature0, feature1, feature2, cme,1500);
  if (norm(d[0] - de[0]) > threshold) {
    if (de[2] < threshold) {
      color([1, rnd(), rnd()]) ring(de);
      echo(" Found Random State solution ",de);
    }
    else {
      echo(" Found no Random State solution in time ");
    }
  }
}

}




 

Intersection Of Lines

Calculate where two lines cross defined by
segments pa1-pa2 and pb1-pb2 

Usage:

function  IntersectionOfLines(pa1, pa2, pb1, pb2)=
let(
da = [(pa1.x-pa2.x),(pa1.y-pa2.y)], 
db = [(pb1.x-pb2.x),(pb1.y-pb2.y)],
the = da.x*db.y - da.y*db.x                 )
(the == 0)? 
undef: /* no in tersection*/
let (
A = (pa1.x * pa2.y - pa1.y * pa2.x),
B = (pb1.x * pb2.y - pb1.y * pb2.x)         )
[( A*db.x - da.x*B ) / the , ( A*db.y - da.y*B ) / the]
;

// demo code
pa1=[rnd(100),rnd(100)];
pa2 =[rnd(100),rnd(100)];
pb1=[rnd(100),rnd(100)];
pb2=[rnd(100),rnd(100)];
I=IntersectionOfLines(pa1, pa2, pb1, pb2);
line(pa1, pa2);
line(pb1, pb2);


// show in red if intersecting 
// else extend linese outside segments
if(I.x>min(pa1.x,pa2.x)&&I.x<max(pa1.x,pa2.x)
&&I.y>min(pa1.y,pa2.y)&&I.y<max(pa1.y,pa2.y))
{color("red")translate(I) sphere(3);
}
else{
translate(I) sphere(3);
hull(){
translate(I) sphere(0.5);
translate(pa1) sphere(0.5);}
hull(){
translate(I) sphere(0.5);
translate(pb1) sphere(0.5);}
}


echo(I);

module line(p1,p2){hull(){
translate(p1) sphere(1);
translate(p2) sphere(1);
}}

function rnd(a = 1, b = 0, s = []) =
s == [] ?
  (rands(min(a, b), max(
    a, b), 1)[0]) :
  (rands(min(a, b), max(a, b), 1, s)[0]);
 

Find if a point is inside of a rectangle

Test if point is within the  rectangle with corners b - c
Usage: 

echo( InRect([1,1],[0,0],[2,3]));
echo( InRect([3,1],[0,0],[2,3]));

 function InRect(point, b, c)= 
   (point.x >= min(b.x, c.x) && point.x <= max(b.x, c.x)
   && point.y >= min(b.y, c.y) && point.y <= max(b.y, c.y)) ; 

Trinagle by side lenghts

Construct a triangle by its side lengths.
first length given will be used as the base.
Usage:

polygon(TrinagleBySides(rands(5, 30, 1)[
  0], rands(5, 30, 1)[0], rands(5,
  30, 1)[0]));

function TrinagleBySides(A, B, C) =
isValidTriangle(A, B, C) ? [
 [0, 0], [A, 0], CCintersection(A, B, C)
  ] : [];

function isValidTriangle(a, b, c) = (

a >  max(b, c)) ?  (a < b + c) : 

(b > max(a,  c)) ? (b < a + c) :

 /*else*/          (c < a +  b);

function CCintersection(A, r0, r1) =
let (p0 = [0, 0], p1 = [A, 0], d = norm(
  p1 - p0), a = (r0 * r0 - r1 * r1 +
  d * d) / (2 * d), h = sqrt(r0 * r0 -
  a * a), p2 = [p0.x + a *
  (p1.x - p0.x) / d, p0.y + a * (p1.y -
    p0.y) / d], p3 = [p2.x + h *
  (p1.y - p0.y) / d, p2.y + h * (p1.x -
    p0.x) / d])
p3;
 

Merge sort

Contributed by arpruss.
Usage: 

function _slice(a,start,end=undef) =
    let(end = end==undef ? len(a) : end)
        start>=end ? [] : [for (i=[start:end-1]) a[i]];

function _mergeLists(a,b,merged=[]) =
    len(a)==0 ? concat(merged,b) :
    len(b)==0 ? concat(merged,a) :
    a[0] < b[0] ? _mergeLists(_slice(a,1), b, merged=concat(merged,[a[0]])) : 
        _mergeLists(_slice(b,1), a, merged=concat(merged,[b[0]]));

function mergeSort(a) =
    let(l=len(a))
        l <= 1 ? a :
        let(split=floor(l/2),
            b=_slice(a,0,end=split),
            c=_slice(a,split))
            _mergeLists(mergeSort(b),mergeSort(c));

echo(mergeSort(rands(0,100,1000)));

n choose k

Find the number of ways one can select k items from a collection of n items.
Usage:

echo(choose(17,13));

function choose(n, k)=
     k == 0? 1
    : (n * choose(n - 1, k - 1)) / k;
 

Koch snowflake

Koch snowflake

Usage:

K=concat(
koch([-100,100],[-100,-100],i=5),koch([-100,-100],[100,-100],i=5),
koch([100,-100],[100,100],i=5),koch([100,100],[-100,100],i=5));
polygon(K);
echo(K);
function koch(p0=[0,0],p4=[100,0],i=5)=i>0?let(
v=(p4-p0),p1=p0+v*1/3,p3=p0+v*2/3,
c=(p4+p0)/2,h=(1/2) * sqrt(3) * norm(v)/3,
perpendicular=[-v.y,v.x],p2=c+(perpendicular/norm(perpendicular)*h))
concat(koch(p0,p1,i-1),koch(p1,p2,i-1),koch(p2,p3,i-1),

koch(p3,p4,i-1)):[p0,p4];
 

Challenge. Can you make this?:

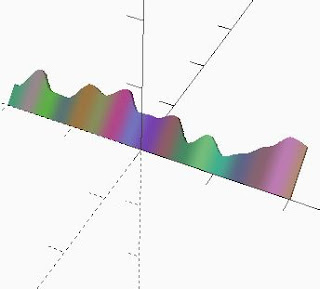
1 dimensional noise

Singel dimension noise layered in three octaves.
Return value is 0-1.
Usage:

seed=rnd(12);
for (a=[-15:0.1:15])  translate([a,0,0])  cube([0.1,0.1, noise_1d(a+seed)]);

function  noise_1d(i,
low_range=1/4,mid_range=1,hi_range=8,
low_magnitude=1/2,mid_magnitude=0.25,hi_magnitude=0.5)=
 (  
single_noise_1d(i/low_range)*low_magnitude+
single_noise_1d(i/mid_range)*mid_magnitude+
single_noise_1d(i/hi_range)*hi_magnitude

)/(low_magnitude+mid_magnitude+hi_magnitude);


function single_noise_1d(i)=
let(
a=floor(i),
b=ceil(i),
c=smooth_curve(i-a),
arnd=rnd(1,0,a),
brnd=rnd(1,0,b),
out=lerp(arnd,brnd,c)
)
out
;

function smooth_curve(a) =let (b = clamp(a))(b * b * (3 - 2 * b));
function clamp(a, b = 0, c = 1) = min(max(a, b), c);
function lerp(start, end, bias) = (end * bias + start * (1 - bias));
function rnd(a = 1, b = 0, s = []) = 
  s == [] ? 
   (rands(min(a, b), max(   a, b), 1)[0]) 
  : 
   (rands(min(a, b), max(a, b), 1, s)[0])
  ;